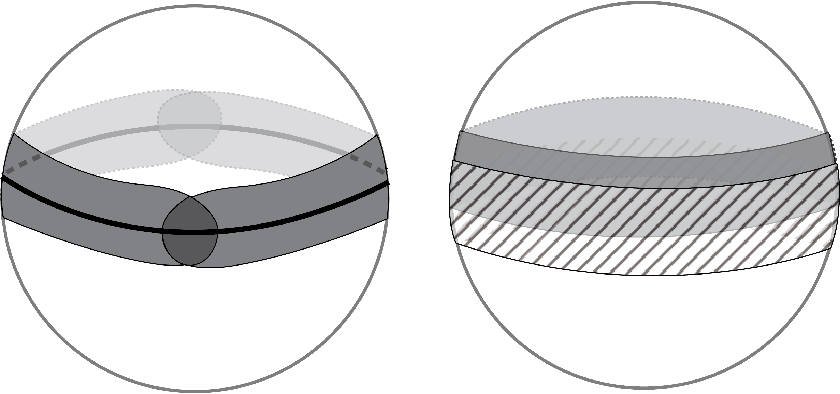
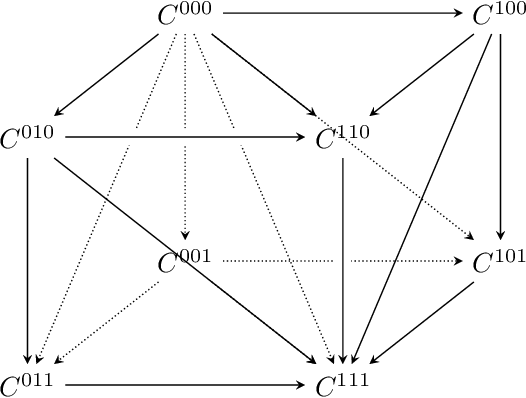
La sucesión de Mayer-Vietoris es una sucesión de grupos de homología exacta. Es de gran importancia en el campo de la Topología algebraica, dado que permite calcular grupos de homología con mayor facilidad. Éste no es el único método, pero en ocasiones puede ser muy simplificador.


Teorema (de Mayer-Vietoris)

Sea X {\displaystyle X} un espacio topológico y U {\displaystyle U} , V {\displaystyle V} dos abiertos contenidos en X {\displaystyle X} tales que X = U ∪ V {\displaystyle X=U\cup V} . Entonces la sucesión:



… ⟶ H p ( U ∩ V ) → φ H p ( U ) ⊕ H p ( V ) → ψ H p ( X ) → Δ H p − 1 ( U ∩ V ) ⟶ … {\displaystyle \ldots \longrightarrow H_{p}(U\cap V){\xrightarrow {\varphi }}\,H_{p}(U)\oplus H_{p}(V){\xrightarrow {\psi }}\,H_{p}(X){\xrightarrow {\Delta }}\,H_{p-1}(U\cap V)\longrightarrow \ldots }
es exacta.


Figure 1 from THE MAYER VIETORIS SEQUENCE CALCULATING DE RHAM

MayerVietoris systems and their applications Papers With Code

Figure 1 from MayerVietoris property for relative symplectic

Victoria Mayer Bild 5 von 13 moviepilot.de

Figure 1 from MayerVietoris property for relative symplectic